Chapter V
Chapter 1 Event Generation and Reconstruction
The startup of the LHC machine will take place in April 2007, and few months will pass before a data sample is ready for analysis. In the meantime, simulations of th e physics processes can be used to tune the physical analysis and forecast the results. Simulation software is composed by a chain of different elements:
- Monte Carlo Event Generators, which compute the matrix elements of the partonic scattering at fixed order;
- Parton Shower Algorithms, which hadronise the scattered partons and simulate the emission of soft gluons and photons in the non-perturbative regime;
- Detector Simulations, which reproduce the effects of the finite resolution of the detector instrumentation on the observables. Detector simulations are of two ty
pes:
- Fast Detector Simulations, where the momenta of the particles are convoluted with parametrised smearing functions;
- Full Detector Simulations, where the interaction of particles with the detector is simulated at the microscopic scale --- resulting in, for example, realistic el ectromagnetic shower shapes, multiple scattering, etc.
The ATLAS collaboration organizes every two years a conference to discuss issues and results of the prospective physics analyses. In preparation for the 2005 confere
nce, held in Rome, a sample of five million events was produced with full detector simulation. As member of the ATLAS Top Physics Working Group, I had the task to ge
nerate a fraction of this sample, dedicated to single top production. In this Chapter I will outline the software framework for the simulation of physics processes i
n ATLAS, the systematic uncertainties in the use of fixed-order Monte Carlo generators, and the data sample for the ATLAS Physics Workshop 2005.
1.1 Monte Carlo Generators
1.1.1 TopReX
The Monte Carlo generator was written with the specific intent of treating top production and decay []. provides production processes not implemented in popular Mo
nte Carlo packages such as Pythia or Herwig. In particular, implements both the Feynman diagrams associated with W-g
luon fusion and takes into account the spin polarization of the decay products of the top quark.
As alread explained in Section ??, the W-gluon fusion channel is described by the interference of a LO and a NLO
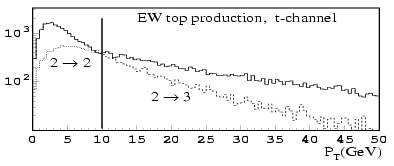
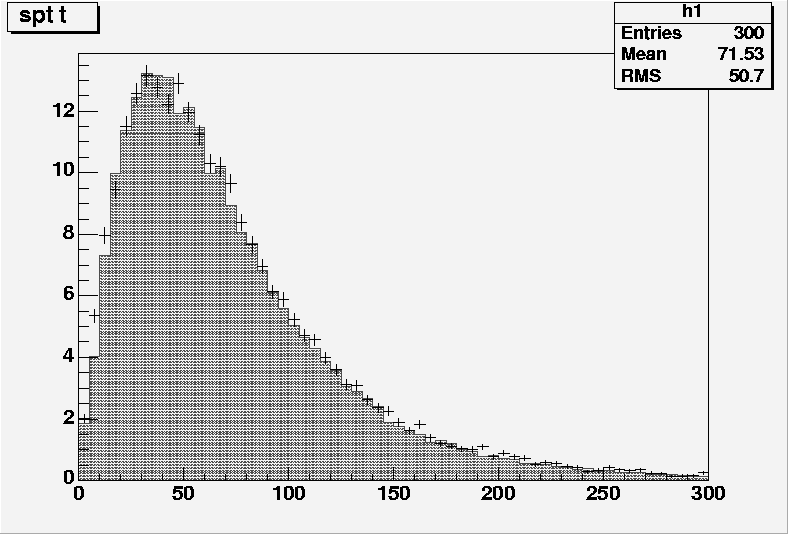
Figure 1.1: pT spectrum of the additional b in the LO 2→2 (dotted curve) and the 2→3 NLO (dashed curve) W-gluon process. The full line shows the spectrum generated by mixing the 2→2 spectrum below the
10 GeV threshold with the 2→3 spectrum above the threshold [].
1.1.2 Comparison with NLO calculation
1.2 Parton Shower Algorithms
Pythia. Brief description of the string model
1.3 Fast simulation
1.3.1 ATLFAST
Atlfast algorithm chain:
- Cell Maker and Clu. All particles are divided in cells of granularity 0.1×0.1 for the barrel and 0.2×0.2 for the endcap. The f angle is smeared accordi ng to two parametrizations of the magnetic fields in the barrel and in the endcap. All cells with Et>1.5 GeV are selected as cluster seeds and listed in descending order. For each seed, all cells inside a cone of D R<0.4 belong to the cluster. A cluster is accepted if the total Et is higher than 10 GeV and the cells used are removed from the list; thus jet energy sh aring is not implemented. Atlfast can also be instr ucted to use kT or sliding window algorithms.
- Isolator. The isolator algorithm associates each reconstructed cluster with a particle of the MC truth. The associated particle must have |h|<2.
5, pt>10 GeV and with a separation D R<0.1 from the cluster baricenter. The particle is
declared as isolated if the associated cluster is atleast D R>0.4 away from the closest reconstructed cluster and the transverse energy depos
ited in a cone D R<0.2 around the particle is lower than 10 GeV. Photons, Electron and Muons follow the same procedure. Muons have a low
er pT threshold (6 GeV) and, in addition, receive a pT smearing. The s
mearing in the Inner Detector is given by The smearing in the Muon Spectrometer is not documented.
δ pT pT =5×10-4⊕0.012 - Jet Maker. Unidentified clusters are treated as hadron jets and smeared with the following (low-luminosity):
δ E E = 0.5 E ⊕0.03 (barrel) For high luminosity, a pile-up term of 7.5 GeV Et is added to non-empty cells. Non-isolateδ E E = 1.0 E ⊕0.07 (endcap) d muons are added to jet energy too. If the total Et exceeds 15 GeV, the hadron jet is accepted.
- Missing Et. The total Et of the event is computed by summing the transv erse momenta of identified isolated particles, hadronic jets, non-isolated muons and unused clusters and cells. The missing Et is obtained by balancing the total Et. Thus it contains neutrinos, SUSY particles (if any) and muons outside the detector acceptance. Since by construction ATLFAST does not add pileup to empty cells, the Missing energy might be a little higher than the true value. .
- Atlfast-B. This algorithm calibrates the jet energy of b-jets, on the premise that b-jets have usually a lower energy than the originating b-quark, because of t he presence of leptons (and hence neutrinos) in the decay chain. This algorithm, moreover, provides a realistic b-tagging and c-tagging efficiency, as opposed to the next to 100% efficiency of the standard ATLFAST algorithm.
1.4 Full Simulation
(Very brief, just an outline on GEANT4 and the Rome Layout)
1.5 ATHENA and the ATLAS Data Model
What do I find inside an AOD?
1.6 The Rome Data Challenge
5 Million events of various nature. Single top samples:
- 100k W-gluon fusion
- 40k+40k Associated production
- 60k s-channel
- 25k+25k W-gluon fusion with FCNC decays
- W+2jets
- W+3jets
- W+4jets
- Wbb
- tt MC@NLO