Revision as of 17:42, 18 July 2005

Chapter 1 The Top Quark

During the past thirty years, physicists have been building comprehensive and accurate models to describe the universe at sub-nuclear level. The result is an elegant set of theories collectively known as the Standard Model (usually abbreviated as SM). These theories provide powerful tools; their predictive power has been confirmed in many experiments worldwide.

The inspiring principle of the Standard Model is gauge symmetry. This principle states that the description of all physical phenomena does not vary if the Lagrangian equations describing the phenomena are subjected to a special set of local transformations --- the local gauge transformations. In analogy with classical mechanics, local gauge invariance in the interaction Lagrangian is associated with conserved currents and boson fields, which act as the medium of the interaction. A great success for gauge theories (and thus for the Standard Model) was the prediction of the properties of intermediate vector bosons W^± and Z⁰, which mediate the weak interaction, and which were discovered at CERN in 1983 [2, 3, 4, 5].

Despite its glorious career, the Standard Model is far from writing the final word in the book of physics: there are several puzzles that still need to be solved and may prove to be a limit to the validity of the Standard Model. The most obvious puzzle is the existence of mass: the electroweak gauge symmetry applies only if the intermediate vector bosons are massless; this of course is contradicted by experimental measurements, which assign to W^± and Z⁰ a mass of 80.425±0.034 and 91.1875±0.0021 GeV respectively [6]. In order to reconcile gauge symmetry and the existence of mass, a spontaneous symmetry breaking mechanism --- known as the Higgs mechanism --- is introduced in the Standard Model. The Higgs mechanism postulates the existence of at least one scalar, electrically neutral boson field --- the Higgs field --- which breaks the electroweak symmetry and interacts with particles. The coupling strength of the interaction of a particle with the Higgs field is proportional to the mass of the particle itself.

The carrier of the Higgs field --- the Higgs boson --- still needs to be found before the Higgs mechanism can be validated; however, the task of finding this elusive particle is rendered more difficult by the fact that the Higgs theory does not predict a value for M_H, the mass of the Higgs boson. Despite this fact, it is still possible to constrain the allowed values of M_H: since the Higgs field is responsible for generating the mass of the electroweak bosons, by measuring precisely the masses of the W^± and Z⁰ one can derive an expectation value for M_H.

The Higgs mass can be constrained by analyzing the one-loop corrections to the mass of W^±: these corrections are proportional to Δ r:

Δ r=Δ r(a,M_Z,M_W,m_t,M_H)=Da-

c_W²

s_W²

Dr+(Δ r)_rem

where Da contains the leading logarithmic contributions from the light fermion loops, Dr contains the m_t² dependence from top/bottom loops and (Δ r)_rem contains the non-leading terms where M_H plays a role [7]. Thus, a precise measurement of M_W and m_t --- the other physical parameters a and M_Z have a smaller impact --- can give us, through the evaluation of Δ r, an estimate on M_H, as shown in Figure 1.1.

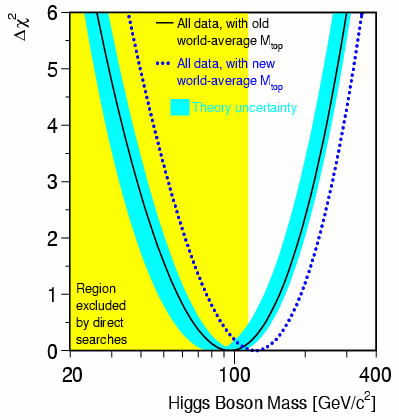
Figure 1.1: χ²-likelihood for the mass of the Higgs boson, depending on the value of the top quark mass. The most probable value corresponds to the minimum χ². The graph shows the shift in M_H for the new Tevatron analyses (dotted line) compared to the previous Tevatron measurements (full line). The band around the full line shows the uncertainties in the theoretical model. Figure taken from [6].

Although the mass of the W^± has been measured with a precision of a few tens of MeV by several experiments over the past twenty years, a measurement of the mass of the top quark with the same degree of precision has not been performed yet. Precise determination of the masses of both the W^± and the top quark are necessary to obtain a good estimate of the Higgs mass.

The top quark was discovered at Fermilab in 1995 [8], and its mass was measured by two experiments, CDF and DØ. The average top mass in Run I was m_t=178.0±2.7±3.3 GeV, and the limiting factors in the mass resolution were uncertainties in the jet energy scale and limited statistics [7]. Hopefully, the statistics will improve once the LHC accelerator starts functioning, pushing top quark physics from the discovery phase to the precision measurement phase. LHC, with its high luminosity, will become a true top factory producing up to 80 million tt pairs per year, allowing us to refine the top mass measurement to a precision of ~1 GeV [7].

Although statistically important, pair production is not the only process by means of which top quarks can be produced at the LHC; there is also so-called single top production, where a single top is present among the final state particles. This process may play an important role in the measurement of m_t: as only one top is present in the final state, the assignment of decay particles is simplified whereas in pair production one has to find the correct assignment of decay products for both the t and the t. Hence the systematic error in the measurement of the top mass, due to the incorrect assignment of decay products, may be reduced, resulting in a more precise measurement.

Another interesting property of electroweak single top production is the cross-section, which is proportional to the CKM matrix element V_tb. A precise measurement of the cross-section for this class of processes may confirm the unitarity of the CKM matrix, or give an indirect evidence for the existence of a fourth quark generation, mixing with the (t,b)_L doublet.

1.1 Properties of the top quark

The top quark was postulated in the Standard Model to complement the bottom quark in the third generation doublet; the model predicts an up-like quark, with spin=1/2, weak isospin=1/2 and charge=+2/3. Results from b-physics at LEP --- for example, the precision measurement of the Z→ bb partial width --- constrains the top mass to a value around 170 GeV [10].

Several properties of the top quark were studied during the first run at Tevatron:

the tt production cross section;
kinematics of the tt pair;
the top mass;
the nature of the V-A electroweak coupling by determining the helicity of the W produced in the decay of the top quark;
spin correlations in tt production;
electroweak production of top quarks;
t decays of the top quark;
exotic decays;
decay channels involving Flavour Changing Neutral Currents.

Results at the Tevatron were hampered by low statistics. The studies will proceed, with evident benefits from increased luminosities, both for Tevatron Run II and at the LHC.

Among the Tevatron studies, the most interesting concerns the mass of the top quark: the combined measurements [9] of the CDF and DØ experiments at the Tevatron at Run I resulted in a top mass of 178.0±4.3 GeV (see Figure 1.2). Such a large mass is quite extraordinary in the the quark hierarchy: the top quark is roughly 35 times more massive than the b quark.

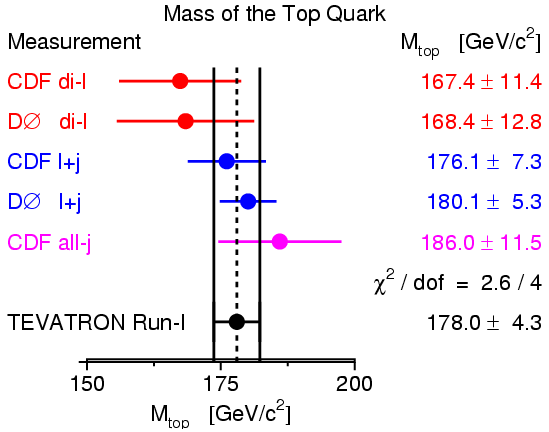
Figure 1.2: Combined measurement of the top quark mass at the Tevatron during Run I. The Run I average includes measurements from lepton-plus-jets and di-leptonic decay channels for both CDF and DØ, plus the CDF jets-only channel. Figure taken from [9].

In the Higgs model, the top quark (like any other fermion) acquires mass via the Yukawa coupling to the Higgs field:

m_t=y_t

v

2

where y_t is the strength of the Yukawa coupling between the top quark and the Higgs field, and v is the vacuum expectation value that is the energy associated to the Higgs field in the vacuum. The Yukawa coupling factor for the top quark y_t is close to unity; this suggests that the top quark may play an important role in models describing the fermionic masses. The Higgs model, however, cannot (yet) explain why the Yukawa coupling of the top quark is so large compared to other quarks; Technicolor models, instead, provide both a dynamical breaking of the electroweak symmetry and a theory for fermion masses. One of these models, the Topcolor-assisted Technicolor (usually referred to as TC2), predicts the existence of a new interaction that couples only with the third quark family [19] and generates the large top mass.

This large mass provides a large phase space in the top decay, which results in a lifetime of 4×10^-25 seconds, an order of magnitude shorter than the characteristic QCD hadronisation time of 28×10^-25 seconds. This has some interesting experimental and theoretical aspects:

with the exception of the 1S ground state, toponium resonances cannot be formed because of the short lifetime of the top quark [16];
hadronisation will not degrade the mass measurement of top quark; however, this effect is spoiled by the fact that the majority of the decay products hadronise;
since the time constant for spin-flip via gluon emission is longer than the lifetime of the top quark, decay products --- in particular the W boson --- retain the spin information of the original top quark [7];
pair production at threshold is not affected by non-perturbative QCD contributions, thus the threshold shape can be predicted by perturbative QCD [17].

Top quark production in tt pairs (see Section 1.2) has a larger cross-section than electroweak single top production (see Section 1.3).

1.2 Top pair production

At the tree level, the cross section for QCD tt production is expressed as: Failed to parse (unknown function "\h"): {\displaystyle \sigma(s,m_t) = \sum_ \int_0^1 dx_1 \int_0^1 dx_2 \, f_i(x_i,\mu^2_f) \, f_j(x_j,\mu^2_f) \; \h(\h,m_t,\alpha_s(\mu^2_r)) } This equation descends from the following assumption: the QCD scattering process can be expressed by independent --- factorised --- terms. Consider the scattering of two protons: they are complex objects, made of several components called partons. The fractional momentum x carried by the partons inside the protons is described by probability density called Parton Distribution Functions --- PDF, indicated by f(x,µ_f²) in the equation. However, when we consider the scattering process, we assume that the scattering partons are independent from the protons that contained them; then, we have factorised the matrix element of the scattering of the two partons from the PDFs that contained the partons. By doing so, we choose an energy scale µ_f, the factorisation scale that separates the description of the parton as a statistic variable from the description of a pointlike particle in the scattering process. In the factorization scheme, the partonic cross section for tt production s depends only on the square of the partonic center of mass energy s=x_ix_js, the top mass m_t and the running strong coupling constant a_s(µ_r²). The coupling constant is evaluated at the renormalisation scale µ_r, that sets the energy limit above which the hard scattering is assumed to be independent from hadronisation effects.

Although the cross-section should be independent from the factorisation and renormalisation scales, the calculation of the scattering matrix element up to finite order introduces an unphysical dependence. At Leading Order (LO) the tt cross section is usually evaluated with µ_f=µ_r=m_t, and has an uncertainty of about 50%. The scale-dependence of the cross section can be reduced if we perform Next-to-Leading Order (NLO) calculations of the same cross section: the expected cross-section at the LHC energy scale increases of 30%, the factorisation scale dependence reduces to 12% [7].

NLO calculations, however, are still affected by the problem of resummations: truncating the calculation of the cross section to some fixed order n of a_s gives reliable results only if the physics processes included in the calculation happen at roughly the same energy scale. When two or more very different energy scales Q,Q₁ are involved in the calculation, the effect of logarithmic terms of the type (a_sln(Q/Q₁))ⁿ⁺¹ has to be included in the computation [7]. Inclusion of these logarithms in the cross-section is called resummation.

There are several classes of logarithms that need to be resummed to calculate cross-sections of heavy quark production processes:

small-x logarithms; these logarithms appear in the cross-section calculations when the center of mass energy s of the colliding partons is several orders of magnitude larger than the energy scale Q of the hard scattering; the extrapolation of PDFs between the two energy scales results in large logarithms ln(s/Q);
bremsstrahlung logarithms; these are connected to the emission of soft collinear gluons by scattered particles;
threshold logarithms of the type ln(1-x); these appear when the final state particles carry a large fraction of the center of mass energy. These logarithms have a sizeable effect for tt production at the LHC: this process obtains its main comntribution from gluon-gluon fusion (see Figure 1.3), and gluon PDFs reach large values for small x, such as at the tt threshold:

x=

2m_t

s
~0.025;
transverse momentum logarithms that occur in the distribution of transverse momentum of systems with high mass that are produced with a vanishing p_T in the LO process.

Resummation of logarithms is performed by introducing a conjugate space to the phase space and performing a transformation of the cross-section equation in the conjugate space. By a proper choice of the conjugate space, the logarithms of the transformed cross-section can be summed in an exponential form factor. Applying an inverse transformation to this form factor results in the correction to the fixed-order cross section.

Resummations performed on the tt cross-section [7] show that Next-to-Leading Logarithm (NLL) corrections applied to NLO diagrams further reduce factorisation scale dependence by 6% (see Table 1.1). It is important to note that resummations do not only affect the absolute value of the cross-section, but the kinematical properties of the process as well. For example, transverse momentum logarithms are associated with the emission of soft gluons in the initial state; a comparison of the p_T spectrum for low-p_T tt pair between NLO predictions and Montecarlo shower algorithms --- which reproduce faithfully soft and collinear gluon radiation --- can point out whether resummation is needed or not.

Factorisation scale

(µ_f=µ_r) NLO NLO+NLL

m_t/2 890 883

m_t 796 825

2m_t 705 782

Table 1.1: Resummation correction to the total tt cross-section (pb) and residual factorisation scale dependence. Numbers taken from [7].

Top pair production at hadron colliders proceeds via the QCD processes qq→ tt and gg→ tt (see Figure 1.3). The two processes have a different relative importance for Tevatron and LHC: when we consider tt production at threshold, the colliding partons need to have a minimum fractional momentum of x=2m_t/s in order to produce a tt pair. Substituting in this equation the center of mass energies of the two colliders, one obtains x~0.2 for Tevatron and x~0.025 for LHC; collisions at the LHC occur in a region where colliding partons carry a small fraction of the momentum of the incoming particles. Small-x regions in Parton Distribution Functions (see below) are mainly populated by gluons, hence at the LHC tt production occurs mainly via gluon-gluon fusion, while at the Tevatron quark/anti-quark annihilation is the most important process.

Figure 1.3: Leading order Feynman diagrams for tt production via the strong interaction. Diagram a). quark-antiquark annihilation, is dominant at the Tevatron, while diagrams b) and c), gluon-gluon fusion, give the largest cross-section at the LHC.

1.3 Single top production

Single top production probes the weak coupling of the top quark with the down-type quarks (d,s,b); at the LHC energies the cross section for single top production is about one third of tt pair production, thus providing the opportunity to obtain adequate statistics for precision measurements in the electroweak sector, which cover the following topics:

the cross-section of single top production processes is proportional to the square of the CKM element V_tb; direct measurement of this parameter has not been performed yet, and violations of the unitarity of the 33 CKM matrix may point to the existence of a fourth quark generation;
lower particle multiplicities in the final state of single top processes reduce combinatorial effects in the reconstruction of the top quark, giving a precision mass measurement complementary to the one obtained from tt processes;
single-top processes constitute a background to other processes of interest, such as tt production or Higgs production;
single top quarks are produced with almost 100% spin polarisation; by measuring the spin polarisation of the top decay products, the V-A coupling of the Wtb vertex can be evaluated;

There are three dominant single top production mechanisms: the s-channel, the t-channel and the associated production, illustrated in Figure 1.4.

At the Tevatron, s-channel production has the largest cross-section, while associated production is negligible; at the LHC the situation is reversed: because of the large gluon density at small x, both associated production and gluon-boson fusion have larger cross-section than the s-channel process, with gluon-boson fusion having the largest cross-section of all three processes (see Table 1.2).

Process Tevatron Run 1 Tevatron Run 2 LHC (t) LHC (t)

s_s-chann^NLO (pb) 0.380± 0.002 0.447± 0.002 6.55± 0.03 4.07± 0.02

s_t-chann^NLO (pb) 0.702± 0.003 0.959± 0.002 152.6± 0.6 90.0± 0.5

s_assoc.^LL (pb) - 0.093± 0.024 31_-2⁺⁸ 31_-2⁺⁸

Table 1.2: Single top quark production cross sections --- table taken from [10].

Figure 1.4: Tree-level Feynman diagram for single-top production processes: (a) s-channel, (b,c) t-channel, (d,e) associated production with a W.

1.3.1 Single top production in the s-channel

The s-channel process (fig. 1.4.a) proceeds via a virtual time-like W boson that decays in a tb pair.
This process probes the kinematic region q²³(m_t+m_b)². The cross-section for this channel at the LHC is much smaller than for the t-channel process; however, the cross-section for this process is known to a better precision, since the initial state involves quark and anti-quarks, the PDFs of which have been accurately measured. Moreover, the quark luminosity can be constrained by measuring the similar Drell-Yan process qq→ W^*®n [7].

Calculations of the NLO cross-section have been performed, which show a dependence on factorisation and renormalisation scales of about 2%, and resummation effects add another 3% to the uncertainty, while the Yukawa corrections from loop diagrams involving the Higgs field are negligible. It has been shown, however, that uncertainties in the measurement of m_t of ±5 GeV result in uncertainties in the cross section of 10%. Overall, taking into account predicted statistical errors and theoretical uncertainties, the measurement of the s-channel cross-sections presents the most favourable method of evaluating the CKM matrix element V_tb.

1.3.2 Gluon-boson fusion

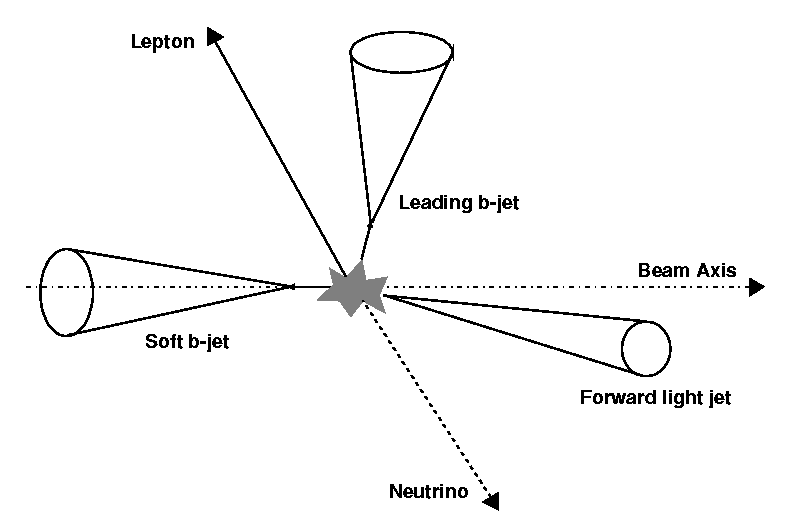
The t-channel process is also known as gluon-boson fusion since in this process a b-quark from a gluon splitting interacts with a space-like W to produce the top quark. The gluon-boson fusion process is the channel with the largest cross-section for single top production at the LHC, about 23 times larger than the cross-section of the s-channel. At the Next-to-Leading-Order level, the process is composed by two diagrams, shown in Figure 1.4(b,c). Both diagrams depict a b-quark interacting with a W boson --- emitted by the colliding parton --- to produce a top quark; diagram (b) depicts a b-quark from the quark sea inside the proton, while diagram (c) is a NLO correction to diagram (b) and is relevant if instead we consider the b-quark in the initial state as the product of a splitting gluon, where the splitting bb pair has a non-vanishing transverse momentum. When the bb pair is collinear with the emitting gluon, diagram (c) becomes a non-perturbative process that can be included in the b-quark PDF; the NLO corrections in this kinematical region have to be subtracted from the computation to avoid double counting of such a diagram. The two diagrams (b) and (c) have the same experimental signature --- a forward scattered light quark, a W and a b-quark --- since the additional b quark from diagram (c) has 75% of the events p_T< 20 GeV, thus hardly observable [10].

The NLO cross-section for the t-channel has a worse scale dependence than the s-channel, with about 5% uncertainty. The top mass uncertainty contributes for 3% when the top mass is changed by ±5 GeV. Yukawa corrections are small (of 1% order) [10].

1.3.3 Associated production

In this production channel, the single top quark is created together with a real W boson. Two Feynman diagrams --- depicted in Figure 1.4(d,e) --- contribute to this channel. However, the t-channel diagram (e) has a smaller contribution since this diagram describes the splitting of a gluon into a tt pair and is mass-suppressed; thus the initial state is affected by the low gluon density at high-x values. The s-channel diagram (d) dominates the associated production; the 1/s scaling of this process, combined with the small b-quark density, result in a negligible cross-section at the Tevatron, while at the LHC it contributes to about 20% for the total single top production.

A subset of NLO diagrams has been computed for this production channel. Gluons in the in initial state splitting into a collinear bb pair have been included in the b-quark PDF, similar to NLO corrections to the t-channel. It must be remarked that one of the corrections corresponds to the strong production process gg→ tt, followed by top quark decay. This diagram represents a background for the associated production channel, and should be subtracted from the cross-section computation [7]. The cross-section has a strong dependence on both PDFs and renormalisation scale, and the total uncertainty is of the order of 30% (see Table 1.2).

1.4 Top quark decay

In the Standard Model, the top quark predominantly decays into a b quark and a W with a branching ratio of 0.998. Aleph and Opal conducted searches for Flavour Changing Neutral Currents (FCNC) decays, which resulted in upper limits for t®g q and t→ Zq of respectively 0.17 and 0.137 [13]. Other SM-allowed decays to down-like quarks are very difficult to disentangle from the QCD background, as opposed to a b-tagged jet. Non-SM decays, however, may provide suitable experimental signatures.

The extension of the SM Higgs sector could induce new channels for the top decay. In the so-called two-Higgs double models (2HDM), the Higgs sector is composed of two neutral scalars (h,H), a neutral pseudo-scalar (A) and two charged scalars (H^±) [10]. In this hypothesis, the top quark could decay into a charged Higgs: t→ bH⁺. Both CDF and DØ have performed indirect searches in Run I data. No evidence has been found, but searches will continue at Run II. A direct measurement of this channel may be performed searching for the signature H^±®tn, while a heavier charged Higgs decaying to quarks will suffer from QCD jet background.

The 2HDM model usually postulates that the charged Higgs should couple preferentially with third-generation quarks due to their large mass. When this assumption is relaxed, new decay channels of the top quark involving Flavour Changing Neutral Currents may emerge: t→ cV_i⁰V_j⁰ at tree level and t→ cV⁰ at one-loop --- V⁰ indicates either g, Z or g. However, the signatures of these channels are very hard to disentangle from QCD background.

1.5 Top detection

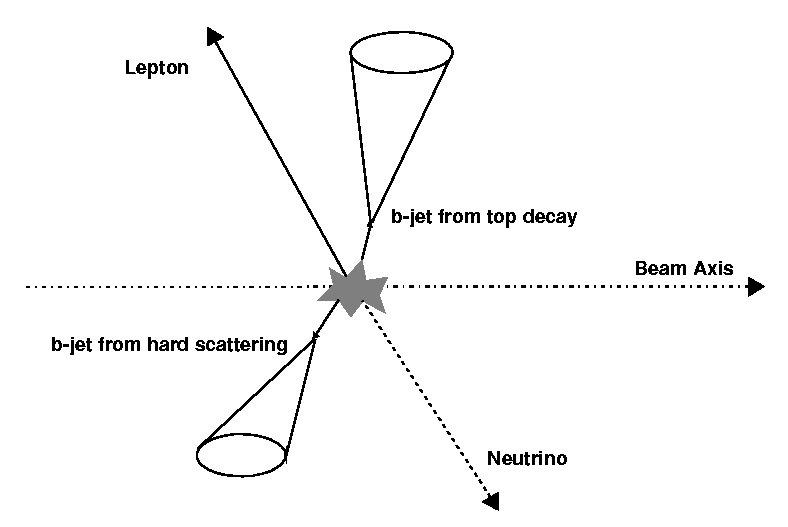
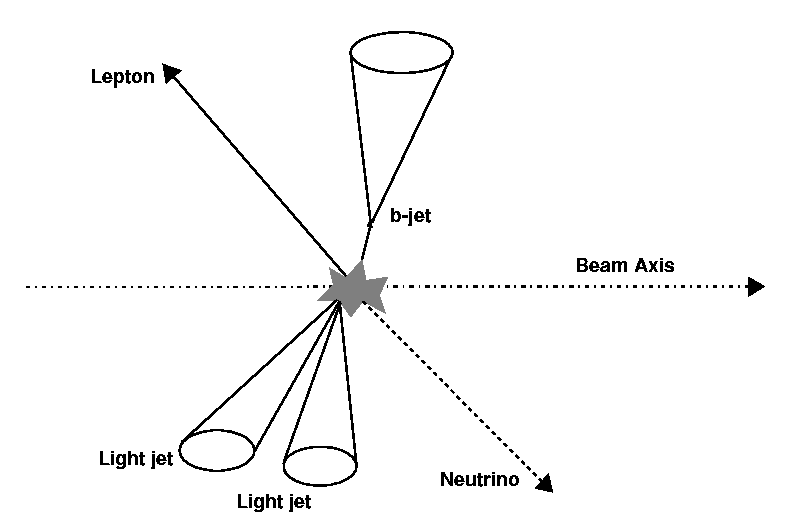
Top quarks in the SM decay almost exclusively into Wb. Because of fermion universality in electroweak interactions, the W boson decays 1/3 of the time into a lepton/neutrino pair and 2/3 of the time into a qq pair. Since in tt events two real W bosons are present, the signatures of the events are classified according to the decay channel of the W bosons:

all jets channel: Here both Ws decay into a quark/anti-quark pair. The event has at least six high-p_T jets, two of which have to be b-tagged. Despite having the highest branching ratio (44%), this decay channel suffers heavily from QCD background and ambiguities in the assignment of jets to the originating Ws.
lepton+jets channel: In this decay channel one W decays into a lepton--neutrino pair, the other W into a quark/anti-quark pair. One isolated lepton, four jets (two with b-tagging) and missing energy characterise the event. The branching ratio is about 30%.
di-lepton channel: In this decay channel, both Ws decay into a lepton--neutrino pair. For practical purposes, only e,µ are considered, since t decays are difficult to distinguish from the QCD background. The events have two high-p_T leptons, two jets (at least one of which is b-tagged) and missing energy due to the neutrinos. This signature is quite clear, being affected mainly by electroweak background. The only drawback of this decay channel is its low branching ratio (5%).

1.6 Event selection and backgrounds

Top quark pairs are produced near threshold and have low kinetic energy, thus present little or no boost in the beam direction. Since the decay products of the top quark have a much smaller mass than the top quark itself, they typically carry large transverse momentum and cross the central region of the detector (|h|<2.5); the low boost from the decaying top accounts for good angular separation of the decay products. If di-lepton or lepton+jets channels are considered, a large missing energy E_T^miss is part of the signature. Experimental cuts on p_T and E_T^miss alone are sufficient to strongly reduce the QCD background, which has an exponentially-falling E_T spectrum and small E_T^miss [10]. Tagging one or more b-jets (either by secondary vertex or soft muon tagging) further reduces background from QCD.

In addition to the above cuts, further selections can be performed according to the topological features of top production and its decay channels: for example, semi- and fully leptonic decays present one or two high-p_T isolated leptons; topological variables such as H_T (the scalar sum of the E_T of all observed objects), sphericity (S) and aplanarity (A) can be employed to discriminate against QCD background.

1.6.1 Top mass determination in tt events

The selection cuts used at CDF in the lepton+jets sample require [23]:

one isolated lepton with p_T>20 GeV;
missing energy E_T^miss>20 GeV;
at least three jets with p_T>15 GeV and |h|< 2 and one jet with p_T>8 GeV and |h|< 2, with at least 1 b-tagged jet;

--- or ---
at least four jets with p_T>15 GeV and |h|< 2 and no b-tagging requirement.

The selected events are subjected to a kinematical fit, with the constraints M_jj=M_n=M_W and M_t=M_t; of the possible 24 combinations --- 12 if b-tagging is included --- the one with the lowest χ² is chosen; the reconstructed top masses are histogrammed and fitted with signal and background templates, where the signal templates vary according to the mass; the mass that provides the best likelihood in the fit determines the final result.

Top mass measurements in the lepton+jets channel at DØ employ both a reconstruction technique similar to the one described above and a likelihood method. This method examines the kinematical features of each event, and compares them with a template based on sample events generated at the tree-level by the simulation package VECBOS, both for tt production (signal) and W+4j (background), and convoluted with a transfer function that models fragmentation and detector effects. The probability for each event to be a background or a signal event is then used to compute the likelihood for the top quark to have a given mass.

Selection cuts at ATLAS require [21]:

one isolated lepton with p_T>20 GeV and |h|< 2.5;
missing energy E_T^miss>20 GeV;
at least four jets with p_T>40 GeV and |h|< 2.5, of which at least 2 are b-tagged jets.

Two of the non-tagged jets are used to reconstruct the W, with the constraint |M_jj-M_W|< 20 GeV; the reconstructed W is combined with one of the two b-jets to form the top quark. Of all jjb possible combinations, either the one which gives the highest p_T to the reconstructed top, or the one with the highest angular separation between the b-jet and the other jets, is assumed to represent the top quark [21]. The efficiency of this reconstruction is estimated to be 5%, with a top mass resolution of 11.9 GeV.

1.6.2 Top mass determination in single top events

Gluon-boson fusion and s-channel production were studied at the Tevatron during Run I, while associated production has a negligible cross-section at the Tevatron (see Table 1.2).

CDF performed an inclusive single top analysis, searching for single top in the W+jets sample, asking for the invariant mass of the lepton, E-0.57em0.19ex/_Tand highest-p_T jet to lie between 140 and 210 GeV. This was followed by a likelihood fit of the total transverse energy H_T. This technique gave a lower limit for inclusive single-top cross section of 14 pb. CDF also performed two separate searches for s- and t-channel production, which resulted in lower limits of respectively, 18 and 13 pb. DØ used neural networks giving lower limits of 17 pb for s-channel and 22 pb for t-channel production.

Since single top experimental signatures show a lower jet multiplicity compared to pair production, stringent cuts are required to isolate single top events; from QCD background; moreover, each of the three single top production processes is a background process for the other two, the cuts need to be tailored to each of the three channels.

The ATLAS reconstruction technique entails a set of pre-selection cuts to reduce QCD background; this set includes [21]:

at least one isolated lepton with p_T>20 GeV;
at least two jets with p_T>30 GeV;
at least 1 b-tagged jet with p_T>50 GeV.

The net effect of these cuts is to select leptonic decay products of the single top. On top of the pre-selection cuts, each channel adds its own set of selection cuts.

s-channel selection cuts

exactly two jets within |h|< 2.5; this cut reduces tt background, which has a higher jet multiplicity;
the two jets need to be b-tagged and have p_T>75 GeV; this cut reduces both W+jets and Gluon-boson fusion, where the second b-jet is either missing or has low p_T;
H_T>175 GeV and total invariant mass greater than 200 GeV; these cuts reduce Wjj background, which tend to have smaller total transverse energy and smaller invariant masses;
reconstructed top mass between 150 and 200 GeV.

Figure 1.5: Experimental signature of single top production in the s-channel.

Gluon-boson fusion selection cuts

exactly two jets with p_T>30 GeV; this cut reduces the tt background;
one of the two jets with |h|> 2.5 and p_T>50 GeV; this cut selects the forward light quark, which is the trademark of the gluon-boson fusion process;
the other jet needs to be b-tagged and have p_T>50 GeV; this cut reduces Wjj background;
H_T>200 GeV and total invariant mass greater than 300 GeV; these cuts reduce Wjj background;
reconstructed top mass between 150 and 200 GeV.

Figure 1.6: Experimental signature of single top production in the gluon-boson fusion channel.

Associated production selection cuts

exactly three jets with p_T>50 GeV; this cut reduces the tt background;
one of the three jets needs to be b-tagged; this cut reduces Wjj background, and further reduces tt background;
total invariant mass less than 300 GeV; this cuts reduces the tt background;
the invariant mass of the two non-b jets between 65 and 95 GeV; this cut enhances the probability that a real W boson is present in the final state.

Figure 1.7: Experimental signature of single top production in the associated production channel.

Efficiencies (%) Wg W^* Wt tt Wjj

Pre-selection 20.0 27.0 25.5 44.4 0.667

Selection 1.64 1.67 1.27

Events/30 fb^-1 26800±1000 1106±40 6828±269

Table 1.3: Efficiencies of the selection cuts for gluon-boson fusion (Wg), s-channel production (W^*) and associated production (Wt) at ATLAS. The pre-selection efficiencies for the two most important background processes, tt and Wjj are given for comparison. Table abridged from [21].

1.7 Performance requirements for top physics

Studying electroweak top production processes at hadron colliders involves the correct identification of the decay chain of the top quark, which may contain the following "ingredients":

highly energetic isolated leptons;
highly energetic hadronic jets;
one or more b-tagged jets;
missing energy from the leptonic decay of the W.

To each item on this list correspond precise requirements on the performance of the detector: a good detector performance results in a higher efficiency for event analyses and lower systematic error on measurements of the parameters involved in the physical process under study.

These requirements include:

correct identification of electrons, photons and pions;
calibrated calorimeter for precise jet energy measurements;
efficient track reconstruction for high-p_t leptons;
tagging of jets originated by b-quarks;
detector coverage up to high pseudorapidity for accurate missing transverse energy measurements.

In the past years, the design of detectors employed at colliders has been optimised in order to fulfil these requirements. The typical detector is composed of several concentric subdetectors, each performing a specific task, and all or part of the detector is immersed in one or more magnetic fields in order to evaluate particle momenta.

The innermost layer of a detector is usually instrumented with silicon trackers. These detectors fulfill the task of tracking the path of charged particles close to the interaction point. The reconstructed tracks can extrapolated back to the interaction point to evaluate the impact parameters or, if the extrapolation leads to a different point, reveal a secondary vertex. Secondary vertices are a signal for long-lived unstable particles, such as the b-quark.

Outside the silicon trackers, the calorimetry system is located. The antiquated term "calorimetry" reflects the purpose of this part of the detector: much like the Dewar bottles with which good old Mister Joule was entertaining himself during his honeymoon, today's calorimeters have to contain and measure the total energy of the interaction. Plus, modern calorimeters give the opportunity to measure individually the energy of each of the particles created in the hard interaction, and to measure their direction. There are two types of calorimeters: electromagnetic calorimeters and hadronic calorimeters. These two types of calorimeters exploit different physical phenomena to measure the energy of the incoming particles: the first type usually deals with electron, photons and the occasional soft pion, while the second type deals with hadrons. A well-designed detector utilises both types of calorimeters.

The calorimeter succesfuly contains all types of particles but two: neutrinos --- which can be detected by measuring an imbalance of energy in the calorimeters --- and muons. Muons deposit a minimal amount of energy in the calorimeters, thus an alternative method is needed for measuring their energy. For this reason, the typical detector is provided with a Muon Spectrometer, located on the outermost layer, outside the calorimeters. The spectrometer uses gaseous detectors, such as drift chambers, to track muons and measure their momentum.

ATLAS is a general-purpose detector designed to be used at the LHC; thus it adheres to the detector design described above. Apart from performance requirements related the physics program, the ATLAS detector is required to cope with the harsh environment created by the LHC accelerator: the detector must operate efficiently in all luminosity regimes, from an initial low luminosity period of 210³³cm^-2s^-1 up to the nominal LHC luminosity of 10³⁴cm^-2s^-1. High luminosity poses a double threat: for each bunch crossing, about 20 proton-proton interactions, most of which are soft elastic collisions (minimum bias events) constitute a background for physics processes of interest. High luminosity also means high levels of radiation around the interaction points and in the forward regions of the detector: these detector elements need to be radiation tolerant in order to keep an acceptable level of performance during the years of operation. In the next sections I will outline the measurement techniques used at ATLAS and the performance they can provide, while the description of the detector and the evaluation of the performance in real-life tests will be laid out in Chapter 2.

1.7.1 Vertex identification and b-tagging

The tagging of b-quarks is a very important tool in the study of top decay processes. Given the high branching ratio for a top to decay into Wb, the requirement of a b-tagged jet is one of the most important analytical cuts to reject backgrounds which have a high jet multiplicity but a low b-jet content (such as W+jets). The b-tagging needs to combine a high rejection power with a high efficiency --- otherwise it would lower the overall efficiency of the analysis.

The b-tagging algorithm in ATLAS is based on the long lifetime of the b-quark: these quarks, on average, decay about 470 µm away from the primary interaction vertex; by measuring the tracks of the decay products is possible to reconstruct the b-decay vertex, and tag the jet formed by the decay products as a b-jet.

For each hadronic jet found in the calorimeter, all tracks measured in the Inner Detector ((see Section 2.2)) with p_T>1 GeV and inside a cone of radius Δ R<0.4 around the jet axis are assigned to the jet. Each track yields two parameters: the impact parameter a₀ and the longitudinal impact parameter z₀. The impact parameter a₀ is the distance between the extrapolated track and the primary interaction vertex in the transverse plane; this parameter is signed: the sign is positive if the extrapolated track intersects the beam axis between the primary vertex and the jet, while it is negative if the track intersects the beam axis behind the primary vertex --- that is, the primary vertex is located between the intersection point and the jet. The longitudinal impact parameter z₀ is the z coordinate of the intersection point, and is signed in the same way as a₀. Montecarlo data has been generated to study the distribution of the impact parameters for u- and b-quark jets; both distributions show a peak at zero (no secondary vertex) and a small tail at negative values (given by particles wrongly assigned to the jet); however, the b-jet distributions for a₀ and z₀ show a tail on the positive side, corresponding to a secondary vertex. The original algorithm --- illustrated in the ATLAS Technical Design Review (TDR) [20] --- used only the impact parameter a₀ (hence it is regarded as 2D-algorithm), while the current algorithm combines the two impact parameters (hence it is called 3D-algorithm).

The a₀ and z₀ parameters of each track are used to compute a significance value:

S(a₀,z₀)=

a₀

s(a₀)

Å

z₀

s(z₀)

where s(a₀) and s(z₀) are the resolutions on the impact parameters.

The distribution of the significances for u-jets and b-jets is shown in Figure 1.8.a. Each track is assigned a value given by the ratio of the significances for the two flavours, and the jet is assigned a weight given by the logarithmic sum of the ratios of the tracks matching the jet:

W_jet=

å

tracks

ln

æ
ç
ç

è

b(S)

u(S)

ö
÷
÷

ø

.

The weight is the likelihood measure for a given jet to originate from a b-quark; by applying a cut on this weight --- optimised to reach 50% efficiency on b-tagging --- it is possible to separate light jets from b-jets. Though it is not possible to investigate the performance of b-tagging algorithms in a test setup, it is possible to apply Montecarlo tools to study detector effects. The likelihood distributions for light and b-jets obtained from the Montecarlo simulation are shown in Figure 1.8.b.

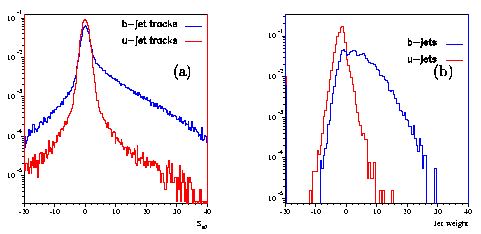
Figure 1.8: a) significance of the impact parameter a₀ for u-jets and b-jets. b) jet weights for u-jets and b-jets [25].

In a recent study [25], the comparison of the performance of b-tagging in a realistic ATLAS environment against the TDR results includes:

changes in the layout of the Pixel Detector (see Section 2.2.1): the initial layout has only 2 pixel layers, the intermediate pixel layer will be installed at a later date; the b-layer has been moved further away from the beam with respect to the TDR layout;
the pixel size in the h direction is increased from 300 to 400 µm;
"ganged" pixels (see Section 2.2.1) are present in the layout;
increase of dead material in the Pixel Detector due to a redesign of detector services;
staging of the wheels of the Transition Radiation Detector (see Section 2.2.3);
simulation of detector inefficiencies: on top of the standard 3% inefficiency for Pixels, SCT strips and TRT straw, the effect of 1% dead pixel modules and 2% dead pixel modules are added;
effects of misalignment between the Pixel Detector and the Semiconductor Tracker (see Section 2.2.2);
addition of minimum bias pile-up events.

The study used samples from tt, ttH, WH (M_H=120 GeV) and WH (M_H=400 GeV), to evaluate the efficiency of the b-tagging algorithm for b-jets over a wide range of pseudorapidity and p_T. The Inner Detector was simulated by GEANT3, while the jets were reconstructed using both ATLFAST and full detector simulation --- the differences were found to be marginal. The results of the study, summarised in Table 1.4, are the following:

changes in the detector layout amount to a reduction in rejection power by a factor 0.5±0.2, mainly due to increase of material in the Inner Detector;
staging of the intermediate layer in the Pixel Detector amounts to a reduction by a factor 0.7±0.1;
pile-up events at low luminosity, realistic detector inefficiencies, and misalignment between the Pixel Detector and the SCT during the detector commissioning stages amount to a factor 0.75±0.05;
changing the pixel size to 400 µm in the b-layer amount to a 10% decrease in rejection;
improved track fitting algorithms increase the rejection power by a factor 1.8; the improved algorithms perform well with high track multiplicity coming from pile-up events at high luminosity: the rejection power is degraded only by 10% at high luminosity;
using the new 3D algorithm instead of the old 2D algorithm increases the rejection power by a factor 1.9; a factor 2.8 can be reached by an improved algorithm [25] which combines the 3D likelihood with other discriminating variables (such as the invariant mass of tracks from the secondary vertex).

Despite the decrease in rejection given by the new layout, improvements in the tracking and tagging algorithms can still provide a rejection factor of about 150 for a b-tagging efficiency e_b=60%, higher than the nominal TDR value of R=100 at e_b=50%. The b-tagging algorithm can realistically achieve R=100 at e_b=70% in the low luminosity regime, increasing the efficiency of all physical analyses based on the identification of b-jets [25].

This study produced also a new parametrization of b-tagging, depending on p_T and h, to be used in conjunction with ATLFAST data.

Algorithm TDR Initial layout

perfect perfect +pile-up +400µm +Ineff 1/2%

2D e_b=50% 300±10 204±6 203±5 200±5 156±4

2D e_b=60% 83±1 62±1 60±1 58±1 49±1

3D e_b=50% 650±31 401±15 387±14 346±12 261±8

3D e_b=60% 151±3 112±2 109±2 97±2 79±1

Table 1.4: Rejection power for the 2D and 3D algorithms, both for TDR and current detector layout. "Perfect" refers to the detector without inefficiencies, no pile-up and with the original pixel size in the b-layer. Realistic effects are added from left to right column, degrading the rejection power. Table taken from [25].

1.7.2 Jet reconstruction

Top production events always include two or more high energy hadronic jets; for a better comprehension of the underlying physics phenomena, it is necessary to understand the connection between the jets and the particles that generated them. However, the definition of a jet is not unique, as different reconstruction algorithms may produce signatures with incompatible characteristics (jet multiplicity, energy etc.). Thus, the choice of the jet algorithm introduces a systematic effect in the measurement.

A jet algorithm should not only give a good estimation of the properties of originating particles, but it should also be consistent both at the experimental and the theoretical levels, in order to facilitate the comparison between experimental results and theoretical or Montecarlo predictions. The ideal jet reconstruction algorithm should include these characteristics [26]:

Infrared safety: the result of the jet finding algorithm does not get affected by soft radiation;
Collinear safety: the jet finding algorithm is not sensitive to the emission of collinear particles;
Invariance under boosts: the algorithm result is independent of boosts along the beam axis;
Stability with luminosity: the algorithm is not affected by the presence of minimum bias events and multiple hard scatterings;
Detector independence: the algorithm performance is independent from the type of detector that provides the data. The algorithm does not degrade the intrinsic resolution of the detector;
Ease of calibration: the kinematical properties of the jet are well-defined and allow calibration.

Jet reconstruction algorithms parse a list of clusters --- which can be made of calorimeter towers in a real experiment or particle clusters in a Montecarlo simulations --- and tries to merge neighbouring clusters into jet candidates. The properties of the merged clusters are processed, according to a "recombination scheme", to produce the kinematical variables of the jet candidate.

There are two types of algorithms for merging clusters: cone algorithms and K_T algorithms.

Cone algorithms

In cone algorithms, a 2-dimensional map of calorimeter cells is scanned, looking for clusters which have a local maximum of deposited energy. These maxima are used as "seeds" for the jet search and stored in a list, ordered by decreasing E_T. For each seed in the list, the algorithm adds sequentially clusters which lie within a distance R from the center of the starting seed --- the distance in the detector frame of reference is defined as Δ R=Dh²+Df², and it describes a cone centered on the interaction point.

At each step of the sequence, the energies of the merged cluster and the jet candidate are summed, and the centroid of the jet is calculated by weighing the coordinates of the clusters with the transverse energy E_T of the clusters. The algorithm stops either when there are no more clusters available or when the cone is "stable", which means that the centroid is aligned with the cone axis [26]. In order to reduce jet multiplicity, a cutoff on the minimum jet energy E_min can be introduced. Jets with energy lower than E_min are rejected by the algorithm.

There two main disadvantages in the use of cone algorithms: first of all, the use of seeds makes the algorithm sensitive to infrared radiation and collinear effects. In the case of infrared emission, the emitted radiation creates additional energy clusters which can be used as jet seeds, biasing the result of the algorithm. A similar thing occurs in the case of collinear radiation, where the bias is caused by the jet energy being spread over different towers by collinear particles. This effects can be solved by seedless cone algorithms [26]. This class of algorithms is however computer-intensive, since the algorithm treats all clusters as possible jet initiators. Another solution is to include in the list of initiatiors the midpoints between the seeds.

The second disadvantage of cone algorithms is the occurrence of overlapping jets. This problem can be solved by introducing the following policy [26]: jets which share a fraction f of their total energy are merged --- typically f=50% --- while for lower fractions the shared clusters are split between the two jets, according to the nearest distance.

K_T algorithms

In the K_T scheme, the algorithm starts with a list of preclusters. This is a list of clusters which have been preliminary merged, for two reasons: to reduce the number of input objects to the algorithm, hence reducing computation time; to reduce detector-dependent effects (for example, merging clusters across calorimeter cracks and uninstrumented regions).

Preclustering can be achieved in several ways: at CDF, cells from the hadronic and electromagnetic calorimeters are combined only if the p_T of the resulting precluster is larger than 100 MeV; at DØ, preclusters are formed by summing cells until the precluster p_T is positive¹ and larger than 200 MeV.

What about ATLAS?

For each precluster combination i,j from the list, the K_T algorithm computes [26]:

d_ij

=

min(p_T,i²,p_T,j²)

Δ R_ij²

D²

=

min(p_T,i²,p_T,j²)

(y_i-y_j)²+(f_i-f_j)²

D²

where y_i, f_i are the rapidity and the azimuthal angle of the cluster i. The parameter D is a cutoff parameter that regulates the maximum allowed distance for two preclusters to be merged. For D»1 and Δ R_ij²«1, d_ij is the relative transverse momentum k_^ between the two preclusters i,j.

The algorithm computes the minimum among all d_ij and the squared momenta of the preclusters p_T,i². If the minimum is a d_ij, the two corresponding preclusters are removed from the list and replaced with a merged cluster. If the minimum is a p_T,i², then the precluster i is identified as a jet and removed from the list. The algorithm proceeds either when the precluster list is empty, or when the minimum falls below a threshold value d_cut.

1.7.3 Jet energy calibration

The calorimeters need to cover the maximum possible h range and have the largest feasible absorption length, to avoid particles escaping detection in non-instrumented areas or "punching through" the detector; a good detector hermeticity allows for the accurate measurements of imbalances in the azimuthal distribution of energy, giving an estimate of the missing energy E_T^misscarried by non-interacting neutral particles, such as the neutrino or its supersymmetric counterpart. Calorimetry is very important for muon detection too, since it can complement the tracking of the Muon Spectrometer with a measurement of the momentum lost by the muons while crossing the calorimeters.

All of the ATLAS calorimeters are segmented in cells over the R,f,h coordinates: each of the cells is read out independently from the others. The segmentation makes it possible to study the characteristics of particle showers generated by the primary particle entering the detector; the position of the showers gives an indication on the direction of the primary particle, while the spatial properties of the shower permits the identification of the primary particle: electrons and photons produce typically shorter and narrower showers, hadron jets produce broader and longer showers, while muons deposit only a modest amount of their initial energy.

The calorimetry system of the ATLAS experiment is divided in an electromagnetic and a hadronic section (see Figure 2.7). The electromagnetic calorimeter is more suited to contain particle showers created by electrons and photons, while the hadronic calorimeters deals with single hadrons --- such as pions, kaons etc --- or hadronic jets.

The energy resolution for all calorimetry systems is expressed by the following formula:

s

E

=

a

E

Å

b

E

Å c.

The term a is due to the stochastic fluctuations on the number of particles in the shower created by the primary particle and to fluctuations on the amount of energy that cannot be measured by the calorimeter. This "invisible" energy includes energy absorbed in the passive material of sampling calorimeters and energy dissipated by physical processes difficult to detect in the calorimeter (such as neutron production, nuclear fission or nuclear excitation); the effect of term a decreases for increasing energies. The term b is the noise term and includes both electronic and detector noise and pile-up events; these events are soft (p_T< 500 MeV) scattering events which accompany the hard collision --- around 20 pile-up events for each bunch crossing at design luminosity are expected --- and deposit a low amount of energy in the calorimeter. The term c is the constant systematic error, which becomes predominant at high energies, and is composed of several contributions:

the difference in the electromagnetic/hadronic response for non-compensating calorimeters;
inhomogeneities in the response of the calorimeter;
miscalibration in the conversion factor between the charge signal measured by the calorimeter and the energy of the primary particle;
environmental effects: temperature gradients across the calorimeter, aging of the detector elements due to irradiation;
leakage of the particle shower through the detector;
degradation of energy resolution by loss of energy of the primary particle outside the calorimeter (cabling, cooling pipes, support structures, upstream detectors).

While the stochastic term and the noise term can be modelled by simulation, the systematic term can be reduced in magnitude only by a better understanding of the real detector. The aim of test beam studies of the calorimetry systems is to evaluate the impact of all three terms on the calorimeter performance, and to obtain a better energy resolution.

1.7.4 e/g identification

The leptonic decay of the W in single top events generates a high energy lepton providing a clear signature for the process. However, there is a chance that electrons may be mistaken for photons and vice versa. A high-p_T electron may lose a fair amount of energy via bremsstrahlung, thus making its track reconstruction impossible; energy deposition in the calorimeter combined with no visible charged track would result in the electron being mistakenly identified as a photon. On the other hand, a photon may convert early to an electron/positron pair, and one of the two track may not be detected, thus wrongly identifying the surviving track as a prompt electron instead of a conversion product.

A technique for the correct reconstruction of electron and photons was explored in the ATLAS TDR [20]: for each cluster in the Electromagnetic Calorimeter, tracks are searched in a cone of radius Δ R<0.1 around the direction of the cluster. The xKalman track reconstruction algorithm is used to identify tracks; this algorithm treats bremsstrahlung emission as a soft continuous correction, thus it cannot cope with hard photon emissions which cause a kink in the track. If tracks are found in the search cone, they are passed to the xConver algorithm; this algorithm scans for opposite charged track pairs that may come from a photon conversion. If no conversion is found, the cluster is identified as an electron. If xKalman does not find any track, a second algorithm PixlRec, which can cope with hard bremsstrahlung, is invoked. The tracks found by PixlRec are again passed to xConver. If either no tracks are found both by xKalman and PixlRec, or xConver flags a track as a result of a conversion, the cluster is identified as a photon. The electron efficiency of this sequence of algorithms is estimated to be 99.8% with a rejection factor against mistagged photons of 18. The photon efficiency is 94.4% with a rejection factor against electrons of about 500 [20].

1.7.5 e/p identification

A low energy pion can create a shower in the electromagnetic calorimeter, while leaving no signal in the hadronic calorimeter. If such a shower is associated by mistake with a charged track in the silicon trackers, the pion can be mistakenly identified as an electron. The detection of Transition Radiation can prevent such an occurrence. Transition Radiation is emitted when a particle traverses a medium with varying dielectric constant. The variation in the constant creates an oscillating dipole that emits X-rays with energy varying from 2 to 20 keV. Detecting X-rays in conjunction with a charged track gives the possibility to perform particle identification: in order to emit the transition radiation, the impinging particle needs to travel in the ultra-relativistic regime, with g~1000 [13] --- that is, 0.5 GeV for electrons and 140 GeV for pions. Thus, the presence of X-ray signal along the particle track is more likely to indicate the presence of an electron track rather than a pion track. It should be pointed out that pions can generate high-energy signals through d-rays; but the choice of a threshold level of 5 keV --- above the expected energy deposition of a d-ray --- minimises pion misidentification [40].

1.7.6 Muon momentum measurement

The measurement of the momentum of a charged particle in a magnetic field is based upon the measurement of the deflection of the particle track by means of the Lorentz force: a charged particle with momentum p in a magnetic field B travels along an helicoidal path; projecting the helix upon a plane normal to B we obtain an arc which radius r is:

r=

|p|

k×|B|

, k=0.3 GeV m^-1T^-1.

Measuring the chord L of the arc and the sagitta s, we have:

rll L

=

2rsinq~ 2rq

s

=

r(1-cosq)~

1

2

rq²=

L²

8r

where q is the angle corresponding to the ratio between the arc length and the full circumference with the same radius as the arc. From this equation we obtain the relation between the relation between the particle momentum and the arc:

p=

0.3B

r

~

0.3BL²

8s

Thus, by measuring the chord and the sagitta of the arc travelled by a charged particle in a known magnetic field, we can determine the particle's momentum.

The ATLAS Muon Spectrometer (see Section 2.4) is located in the outermost region of the detector . The muon momentum is measured using two different techniques:

in the barrel region (|h|<2.5) three concentric layers of precision drift chambers measure the track of crossing muons in three points in space. The chambers are in a 4 T toroidal magnetic field. The sagitta of the bending tracks is calculated by measuring the position of the track point in the middle layer with respect to a straight line connecting the track points in the inner and outer layers.
at high rapidities, three layers of precision chambers are used but only the first layer is in a magnetic field; thus, the particle momentum is evaluated using the "point and angle technique" that consists in measuring the deflection angle between the track segment reconstructed in the first layer and the track segment reconstructed in the outer layers:

p=

0.3× BL

Da

where L denotes here the length of the path travelled by the particle inside the magnetic field.

The resolution of momentum measurement in the Muon Spectrometer is influenced by two independent factors:

a term depending on the spatial measurement of the track points:

æ
ç
ç

è

Δ p

p

ö
÷

÷

ø

sag
µ

p

BL²
s
where s is the intrinsic resolution of the precision chambers. This term is dominant for high momentum muons (p_T>300 GeV);
a term due to multiple scattering of muons:

æ
ç
ç

è

Δ p

p

ö
÷
÷

ø

MS
µ

1

BLX₀
.
This term is dominant for muons with momenta 30<p_T<300 GeV.

The total momentum resolution is given by the above two terms:

æ
ç

ç

è

Δ p

p

ö

÷
÷

ø

2

tot

=

æ
ç
ç

è

Δ p

p

ö
÷
÷

ø

2

sag

+

æ
ç
ç

è

Δ p

p

ö
÷

÷

ø

2

MS

.

The resolution of the Muon Spectrometer was estimated at the test-beam in 2004. The "point and angle" technique was used due to the lack of a large magnetic field to cover three layers of chambers. The results of the tests are summarised in Section 2.4.1.

1: At the DØ calorimeter, the energy deposition from preceding bunch crossings may cause a slightly negative voltage signal in the calorimeter cells

--Barison 19:41, 18 Jul 2005 (MET DST)

Difference between revisions of "Chapter I"

Revision as of 17:42, 18 July 2005

Contents

Chapter 1 The Top Quark

1.1 Properties of the top quark

1.2 Top pair production

1.3 Single top production