Difference between revisions of "Estimate of condensation rate"
(Create page) |
(Move image) |
||
| (5 intermediate revisions by the same user not shown) | |||
| Line 14: | Line 14: | ||
Boltzmann constant k<sub>B</sub> = 1.380649e-23 JK<sup>-1</sup> | Boltzmann constant k<sub>B</sub> = 1.380649e-23 JK<sup>-1</sup> | ||
| − | With the ideal gas law, we calculate the amount of air in the vacuum chamber to be 5.75e-9 mol. At sea level we will assume the atmosphere contains 2% water vapour. So, we get n = 0.02*5.75e-9 = 1.15e-10 mol water in our system. The molar mass M of H<sub>2</sub>O is 18 | + | With the ideal gas law, we calculate the amount of air in the vacuum chamber to be 5.75e-9 mol. At sea level we will assume the atmosphere contains 2% water vapour. So, we get n = 0.02*5.75e-9 = 1.15e-10 mol water in our system. The molar mass M of H<sub>2</sub>O is 18 gmol<sup>-1</sup>. |
| − | For the velocity v of the water molecules, we use v = sqrt(3* | + | === Estimate of light absorption due to water condensation === |
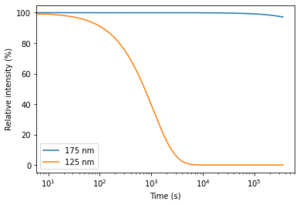
| + | [[File:Condensation.png|thumb|With time, the layer of water gets thicker and more light gets absorbed. This plot shows how much light reaches the sample depending on the time. We assume the water does not deplete and keeps condensing with the same rate (so there must be some outgassing of water).]]For the velocity v of the water molecules, we use v = sqrt(3*R*T/M) = 636 ms<sup>-1</sup> (most probable velocity) and calculate the collision rate per second per square meter as r = 0.5*n*N<sub>A</sub>*v/V = 1.57e18 s<sup>-1</sup>m<sup>-2</sup>. | ||
| − | Now let's calculate how many molecules there will be in a monolayer of water covering our 3cm x 3cm sample. A cm<sup>3</sup> of water has N<sub>A</sub>/18 water molecules, taking the cube root of that gives us | + | Now let's calculate how many molecules there will be in a monolayer of water covering our 3cm x 3cm sample. A cm<sup>3</sup> of water has N<sub>A</sub>/18 water molecules, taking the cube root of that gives us 32222517 layers of molecules, with each 32222517*32222517 molecules. We have 9 cm<sup>2</sup>, so in total 9.3e15 molecules would go into a single layer. |
Using the collision rate and assuming that all molecules that hit the sample will neatly arrange themselves into a single layer as long as there is space, we calculate that it takes 9.3e15/(r*0.03*0.03) = 6.6 s to form a single layer of water on our sample. | Using the collision rate and assuming that all molecules that hit the sample will neatly arrange themselves into a single layer as long as there is space, we calculate that it takes 9.3e15/(r*0.03*0.03) = 6.6 s to form a single layer of water on our sample. | ||
| − | Now, a single layer has a thickness of 1/ | + | Now, a single layer has a thickness of 1/32222517 cm with the same argument as before. So, after 60 seconds we will have a 2.83e-7 cm thick layer of water on our sample. Now, with the Lambert-Beer law, we calculate that at 125 nm, where the absorption coefficient* is 1.978e5 cm<sup>-1</sup>, we have I=100*exp(-1.978e5*2.83e-7) = 94.6% of our light remains and so about 6% is absorbed. At 175 nm the absorption coefficient* is 1.705e1 and therefore 99.999% of our light remains. |
| + | |||
| + | So, how long would it take to lose half our intensity? For 125 nm it will take ~750s (corresponding to an 3.5e-6 cm thick layer of water) and for 175 nm it will take ~100 days (corresponding to a 0.4mm thick layer of water). | ||
| + | === Worst case scenario === | ||
| + | Now, let's compare the above estimate to an absolute worst case scenario. Let's assume all the air in the vacuum chamber is actually water vapour. So, we have 5.75e-9 mol of water. We stick all this water in layers on our sample: so there is nothing left in the rest of the vacuum chamber. Each layer would have again 9.3e15 molecules, which means we get 5.79e-9*N<sub>A</sub>/9.3e15 layers. Each layer is 1/32222517 cm, giving us a water layer of 5.79e-9*N<sub>A</sub>/(9.3e15*32222517) = 1.15e-8 cm thick. Note that this is less than the layer thickness we calculated before after 60 s. Meaning that the above calculation is after 60s actually already worse than this absolute worst case scenario. Of course, we assume here there is no additional outgassing which could make this absolute worst case scenario even worse. | ||
| + | |||
| + | <nowiki>*</nowiki>Absorption coefficients taken from S. G. Warren, "Optical constants of ice from the ultraviolet to the microwave," ''Appl. Opt., 23'', 1026--1225, (1984). | ||
| + | |||
| + | This data is based on the revised 1995 data of Warren. It was revised from the original data in the 1984 paper to account for misinterpretations of data by others. It also includes new data from Kou. | ||
| + | |||
| + | It is for ice, but for water I cannot find the appropriate values for the wavelengths we are interested in. I see other people use this data as well as if it was for water. | ||
Latest revision as of 14:14, 2 August 2023
We want to estimate how quickly a layer of condensation would form on our sample, and how much of the incoming light will be absorbed by this layer. The estimate below is very crude, but serves as a starting point.
Known quantities
Pressure p = 1e-3 Pa (or 1e-5mbar)
Temperature T = 293 K
Volume V = 0.014 m3 (estimated volume of vacuum chamber only)
Gas constant R = 8.314 Jmol-1K-1
Avogadro's constant NA = 6.022e23 mol-1
Boltzmann constant kB = 1.380649e-23 JK-1
With the ideal gas law, we calculate the amount of air in the vacuum chamber to be 5.75e-9 mol. At sea level we will assume the atmosphere contains 2% water vapour. So, we get n = 0.02*5.75e-9 = 1.15e-10 mol water in our system. The molar mass M of H2O is 18 gmol-1.
Estimate of light absorption due to water condensation
For the velocity v of the water molecules, we use v = sqrt(3*R*T/M) = 636 ms-1 (most probable velocity) and calculate the collision rate per second per square meter as r = 0.5*n*NA*v/V = 1.57e18 s-1m-2.
Now let's calculate how many molecules there will be in a monolayer of water covering our 3cm x 3cm sample. A cm3 of water has NA/18 water molecules, taking the cube root of that gives us 32222517 layers of molecules, with each 32222517*32222517 molecules. We have 9 cm2, so in total 9.3e15 molecules would go into a single layer.
Using the collision rate and assuming that all molecules that hit the sample will neatly arrange themselves into a single layer as long as there is space, we calculate that it takes 9.3e15/(r*0.03*0.03) = 6.6 s to form a single layer of water on our sample.
Now, a single layer has a thickness of 1/32222517 cm with the same argument as before. So, after 60 seconds we will have a 2.83e-7 cm thick layer of water on our sample. Now, with the Lambert-Beer law, we calculate that at 125 nm, where the absorption coefficient* is 1.978e5 cm-1, we have I=100*exp(-1.978e5*2.83e-7) = 94.6% of our light remains and so about 6% is absorbed. At 175 nm the absorption coefficient* is 1.705e1 and therefore 99.999% of our light remains.
So, how long would it take to lose half our intensity? For 125 nm it will take ~750s (corresponding to an 3.5e-6 cm thick layer of water) and for 175 nm it will take ~100 days (corresponding to a 0.4mm thick layer of water).
Worst case scenario
Now, let's compare the above estimate to an absolute worst case scenario. Let's assume all the air in the vacuum chamber is actually water vapour. So, we have 5.75e-9 mol of water. We stick all this water in layers on our sample: so there is nothing left in the rest of the vacuum chamber. Each layer would have again 9.3e15 molecules, which means we get 5.79e-9*NA/9.3e15 layers. Each layer is 1/32222517 cm, giving us a water layer of 5.79e-9*NA/(9.3e15*32222517) = 1.15e-8 cm thick. Note that this is less than the layer thickness we calculated before after 60 s. Meaning that the above calculation is after 60s actually already worse than this absolute worst case scenario. Of course, we assume here there is no additional outgassing which could make this absolute worst case scenario even worse.
*Absorption coefficients taken from S. G. Warren, "Optical constants of ice from the ultraviolet to the microwave," Appl. Opt., 23, 1026--1225, (1984).
This data is based on the revised 1995 data of Warren. It was revised from the original data in the 1984 paper to account for misinterpretations of data by others. It also includes new data from Kou.
It is for ice, but for water I cannot find the appropriate values for the wavelengths we are interested in. I see other people use this data as well as if it was for water.